RESULTADOS DOS EXERCÍCIOS

EQUILÍBRIO DE HARDY-WEINBERG

A Genética de populações estuda a estruturação genética de grupos de indivíduos, as populações. Cada população possui um conjunto de indivíduos e estes apresentam diversos tipos de genótipos. A distribuição destes genótipos, determinados a partir da ação do componente genético, é o alvo de estudo.

No início do século XX, de forma independente, Godfrey Hardy e Wilhelm Weinberg (um matemático, o outro médico) propuseram que a distribuição aleatória de gametas em uma população conduzia a uma situação de equilíbrio de frequências nos genótipos dos indivíduos. Este princípio ficou conhecido como Lei de Hardy-Weinberg. Os pressupostos para o equilíbrio Hardy-Weinberg são:

• é infinitamente grande (para eliminar-se a deriva genética);
• realiza reprodução sexuada;
• cruzamentos ocorrem ao acaso = panmixia;
• é diplóide;
• fêmeas e machos ocorrem em igual proporção;
• todos os casais são capazes de reproduzir e geram quantidades equivalemntes de indivíduos na prole.

E não sofre:

• seleção natural
• mutações
• migração (sem fluxo gênico)

Em outras palavras, a população precisa ser infinitamente grande, reproduzir-se aleatoriamente, e também não estar sujeita a ação de forças evolutivas.

constante ao longo das gerações. Desta forma, o equilíbrio genético seria uma consequência direta do processo de segregação que ocorre na formação dos gametas.

Basicamente, em uma população na qual o alelo A ocorre com frequência 0,4 (p) e o alelo a com frequência 0,6 (q), se forem atendidos os pressupostos de Hardy-Weiberg, teremos as seguintes distribuições de genótipos:

1 - AA - para gerar este indivíduo, o genitor masculino deve dar um alelo A e o genitor feminino deve dar o outro alelo A, em uma combinação genética entre alelos A que é única. Assim, AA = frequencia de A (p) x frequencia de A (p) = p x p = p². Em nosso exemplo, f(AA) = 0,4 x 0,4 = 0,24.

2 - Aa - para gerar este indivíduo, o genitor masculino deve dar um alelo A e o genitor feminino deve dar o alelo a, ou, alternativamente, o genitor masculino deve dar um alelo a e o genitor feminino deve dar o alelo A, em duas possibilidades de combinação entre os alelos A e a. Assim, Aa = 2 x frequencia de A (p) x frequencia de a (q) = 2 x p x q = 2pq. Logo, f(Aa) = 2 x 0,4 x 0,6 = 0,48.

3 - aa - para gerar este indivíduo, o genitor masculino deve dar um alelo a e o genitor feminino deve dar o outro alelo a, em uma combinação genética entre alelos a que é única. Assim, aa = frequencia de a (q) x frequencia de a (q) = q x q = q². Em nosso exemplo, f(aa) = 0,6 x 0,6 = 0,36.

Dessa forma, a população apresentará a seguinte distribuição: p² + 2pq + q^2.

DINÂMICA DE CRUZAMENTOS

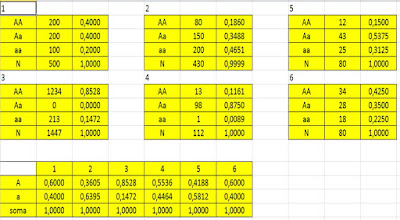
Imagine que em uma população hipotética 20 indivíduos são AA, 50 são Aa e 40 são aa.
Ao calcular as frequências genotípicas e gênicas você observará que:
f(AA) = 0,1818
f(Aa) = 0,4545
f(aa) = 0,3636

f(A) = 0,4091
f(a) = 0,5909

Supondo que o sistema de acasalamneto é panmítico, a próxima geração será constituída por indivíduos gerados nos cruzamentos possíveis nesta população, cujas ocorrências são calculadas como produto das frequências dos genótipos envolvidos. Assim, por exemplo, o cruzamento AA x AA ocorrerá em uma frequência de 0,1818 x 0,1818 = 0,0331. 

Cada cruzamento contribuirá proporcionalmente à sua ocorrência para a composição da próxima geração. Assim, o cruzamento AA x AA, que tem frequência de 0,0331, contribuirá com 0,0331 de indivíduos AA na próxima geração. Já o cruzamento Aa x Aa ocorrerá com frequência de 0,4545 x 0,4545 = 0,2066 e sua contribuição para a próxima geração será de 1/4 AA; 1/2 Aa e 1/4 aa, ou seja, 0,0517 AA; 0,1033 Aa e 0,0517 aa.

As proles geradas em cada cruzamento individual são agrupadas para constituir a próxima geração (F1). Assim, 
f(AA)' = 0,1674
f(Aa)' = 0,4835
f(aa)' = 0,3492

Caso esta nova população (F1) venha a cruzar de forma panmítica, teremos novamente uma próxima geração (F2) constituída por indivíduos gerados nos cruzamentos possíveis nesta população.

Entretanto, agora, não houve alteração na distribuição das frequências.
f(AA)'' = f(AA)' = 0,1674
f(Aa)'' = f(Aa)' = 0,4835
f(aa)'' = f(aa)' = 0,3492

Assim, concluímos que para um locus autossômico, o equilíbrio genético é alcançado após uma geração de panmixia.

material de apoio disponível na internet
http://labs.icb.ufmg.br/lbem/aulas/grad/evol/hwpop.html

ARREDONDAMENTO

http://aprendendoevolucao.blogspot.com.br/2015/08/arredondamento.html

DISTRIBUIÇÃO DE FREQUENCIAS

A Genética de Populações consiste no estudo da origem e do destino da variação genética de um grupo populacional. As premissas adotadas são:
- material genético pode ser replicado
- material genético pode variar (mutar e recombinar)
- o fenótipo resulta da interação do genótipo com o ambiente

Alguns conceitos básicos de genética são importantes:
que tal você buscar uma definição para cada um destes termos e relembrá-los? em caso de dúvida, discutimos em sala, ok?

- gene

- genótipo

- fenótipo

- alelo

- locus

- polimorfismo

- homólogo

gametas geram zigotos

zigotos formam adultos

adultos produzem gametas

A base da genética das populações reside neste paradigma: em termos genéticos, somos o resultado do que foi transmitidos pelos nossos ancestrais, tendo recebido estas informações a partir de nossos genitores.

Uma população é a unidade básica da evolução. Caracteristicamente as populações possuem continuidade genética no tempo (interconexões das gerações sucessivas) e no espaço (intercruzamento dos membros). Isto quer dizer que as informações genéticas, incluindo suas variações, são continuamente intercambiadas ao longo das sucessivas gerações.

Os genes presentes nos indivíduos compõe um conjunto coletivo, o pool genético, que é populacional. Assim, apesar de cada indivíduo consistir em uma unidade genética (uma combinação única de genes), a população é o elemento que apresenta todas as possibilidades e variações para o genoma.

Distribuição de frequências

Para um dado locus, a constituição genética do grupo resulta da distribuição de suas composições genotípicas individuais, ou seja, cada um dos genótipos presentes corresponde a uma parcela (fração) da população

Assim, em um locus autossômico que possui dois alelos (A e a), temos os seguintes genótipos:

AA - cuja frequência é representada por f(AA)
Aa - cuja frequência é representada por f(Aa)
aa - cuja frequência é representada por f(aa)

Como os genótipos são formados a partir de combinações de alelos, podemos identificar no grupo populacional a participação de cada combinação (incluindo as variantes do gene estudado) no conjunto de indivíduos. Assim, as frequências genotípicas refletem a ocorrência de cada um dos genótipos nas estruturação da população. Em uma população com N indivíduos, cada genótipo contará com n(genótipo) indivíduos. O valor de N sempre será dado pela soma dos indivíduos da população.

Por exemplo:

200AA

100Aa

 200aa

N = AA + Aa + aa

N = 200 + 100 + 200

N = 500

f(AA) = n(AA)/N

f(AA) = 200/500
f(AA) = 0,4

f(Aa) = n(Aa)/N
f(Aa) = 100/500
f(Aa) = 0,2

f(aa) = n(aa)/N
f(aa) = 200/500
f(aa) = 0,4

Como os genótipos possíveis para um locus autossômico com dois alelos são AA, Aa e aa, se somarmos suas frequências, obrigatoriamente chegaremos à unidade, ou seja 100% da população. Desta forma,  

f(AA) + f(Aa) + f(aa) = 1,0

Em nosso exemplo, f(AA) = 0,4; f(Aa) = 0,2 e f(aa) = 0,4. Logo,

0,4 + 0,2+ 0,4 = 1,0

A frequência gênica (ou alélica) é definida como a proporção de um determinado tipo de alelo em relação ao conjunto de alelos do locus em questão. O somatório das frequências dos alelos de um locus resulta na totalidade (100%) de alelos. Podemos determinar as frequências gênicas de duas formas, ambas a partir da avaliação dos alelos presentes nos genótipos. Em um método, derivamos a frequência dos alelos a partir das frequências dos genótipos. No outro, determinamos de forma direta a frequência dos alelos na população.

Os  alelos A e a podem, então ter suas frequências calculadas a partir dos dados obtidos no cálculo das frequências genotípicas. OS indivíduos com genótipo AA contribuem integralmente para a frequência do alelo A, ao passo que os heterozigotos (Aa) contribuem apenas com metade de sua frequência. Assim,

f(A) = f(AA) + 1/2f(Aa)

em nosso exemplo, f(AA) = 0,4 e f(Aa) = 0,2. Logo,

f(A) = 0,4 + (0,2/2) = 0,4 + 0,1 = 0,5

O mesmo raciocínio é aplicado para a frequência do alelo a. Assim,

f(a) = f(aa) + f(Aa)/2

f(a) = 0,4 + (0,2/2) = 0,4 + 0,1 = 0,5

Alternativamente, podemos determinar a frequência dos alelos diretamente dos dados obtidos com a genotipagem da população. Como cada indivíduo possui dois alelos (AA, Aa ou aa), determinamos o conjunto de alelos presentes na população.
Em nosso exemplo

200AA correspondem a 400 alelos A

100Aa correspondem a 100 alelos A e 100 alelos a

200aa correspondem a 400 alelos a

O número de alelos em nossa população é, então
400 (oriundos dos indivíduos AA) + 200 (oriundos dos indivíduos Aa) + 400 (oriundos dos indivíduos aa), o que totaliza 1000 alelos.

Assim,
f(A) = 400 (alelos A dos indivíduos AA) + 100 (alelos A dos indivíduos Aa)
f(A) = (400 + 100) / 1000
f(A) = 500 / 1000 = 0,5

f(a) = 400 (alelos a dos indivíduos aa) + 100 (alelos a dos indivíduos Aa)
f(a) = (400 + 100) / 1000
f(a) = 500 / 1000 = 0,5

2016.1

INICIAMOS MAIS UM SEMESTRE LETIVO. IREMOS DISCUTIR OS DIVERSOS ASSUNTOS QUE NOSSA DISCIPLINA ABORDA, INCLUINDO AS TEORIAS EVOLUTIVAS, O SURGIMENTO DA DIVERSIDADE E SUAS IMPLICAÇÕES, A ESTRUTURA GENÉTICA DAS POPULAÇÕES, A AÇÃO DAS FORÇAS EVOLUTIVAS, ENFIM, MUITAS COISAS PARA FALAR

UTILIZAREMOS ESTE BLOG COMO REFERÊNCIA PARA OS TEMAS ABORDADOS EM SALA, COM INDICAÇÃO DE LINKS E/OU RESUMOS DO QUE FOI MINISTRADO.

NOSSOS ASSUNTOS:

- DISTRIBUIÇÃO DE FREQUÊNCIAS E ESTRUTURA GENÉTICA DE POPULAÇÕES

- EQUILÍBRIO DE HARDY-WEINBERG

- AÇÃO DAS FORÇAS EVOLUTIVAS

- LINHAS DE PENSAMENTO EVOLUTIVO

- TEORIAS EVOLUTIVAS

- EVOLUÇÃO HUMANA

 

AVALIAÇÕES

PARA A1 e A2

Prova – 7,0

Atividades (estudos orientados, estudos dirigidos, aulas práticas) – 1,0 CADA, TOTAL 3,0

PARA A3

Prova – 10,0

O uso de calculadora nas aulas e, principalmente, nas avaliações do primeiro bloco é fortemente recomendado. Nas avaliações NÃO SERÁ PERMITIDO O USO DE CELULAR PARA OS CÁLCULOS!

BIBLIOGRAFIA BÁSICA

FUTUYUMA,D. Biologia Evolutiva, Ribeirão Preto: SBG, 2001

STEARN,S.C. e HOEKSTRA,R.F. Evolução: uma introdução, Atheneu, 2003.

BIBLIOGRAFIA COMPLEMENTAR

WILSON, E. Biodiversidade. Rio de Janeiro: Nova Fronteira, 1997

SHORROCKS,B.A. A Origem da Divindade, EDUSP 1980

Site www.aprendendoevolucao.blogspot.com, sob responsabilidade do docente que ministra a disciplina

 

CRONOGRAMA PROPOSITIVO 2016.1